ЗАЧЕТ № 3 НА ТЕМУ: "ГРАФИКА, СИМВОЛЬНЫЕ ФУНКЦИИ, ПРОЦЕДУРЫ И ФУНКЦИИ В ПАСКАЛЕ".

Зачет проводится письменно.

Вариант № 1.

1. Составить программу, рисующую десять вложенных друг в друга кубиков.
   
2. Упорядочить по возрастанию значения четырех переменных a, b, c, d. В программе использовать процедуру, которая меняет местами значения двух переменных.
   
3. Заданы фамилия, имя и отчество учителя, разделенные пробелами. Напечатать его фамилию и инициалы.

Вариант № 2.

1. Используя генератор случайных чисел, нарисовать картинку "звездное небо".
   
2. Составить процедуру для вычисления расстояния r точки М(x,y) от начала координат. Написать программу расчета периметра пятиугольника с координатами вершин A1(x1,y1), A2(x2,y2), ..., A5(x5,y5).
   
3. Выяснить, какая из букв, первая или последняя, встречается в заданном слове чаще.

Вариант № 3.

1. Составить программу, рисующую по главной диагонали (с левого верхнего угла в правый нижний угол) экрана 6 окружностей.
   
2. Вычислить приближенно площадь фигуры, ограниченной осью х, прямыми х=1 и х=3, кривой 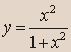, разбивая интервал изменения х на 10 частей, суммируя площади десяти прямоугольников основанием 0,2 и высотой равной значению функции на левой границе его основания. Вычисление функции y(х) оформить в виде функции, а площади прямоугольника в виде процедуры.
   
3. Сколько букв "у" в слове стоит на четных местах?

Вариант № 4.

1. Составить программу, рисующую 10 вложенных эллипсов .
   
2. Треугольник задан координатами своих вершин А, В, С. Проверить равенство площадей треугольников АВР, АСР, ВСР, где Р - точка пересечения медиан треугольника АВС. Проверку осуществить для треугольника А(1,1), B(4,2), C(2,3) и треугольника A(3,2), B(4,2), C(5,3). Вычисление координат точки пересечения медиан оформить в виде функции. Вычисление площади треугольника - в виде процедуры. Координаты точки пересечения медиан:
   XM=(X1+X2+X3)/3; YM=(Y1+Y2+Y3)/3
   Площадь треугольника:
   S=1/2ЧЅ(X2-X1)Ч(Y3-Y1)-(X3-X1)Ч(Y2-Y1)Ѕ
   
3. Проверить, является ли данное слово перевертышем.

Вариант № 5.

1. Составить программу, рисующую на экране 20 дуг разного радиуса и длины.
   
2. Вычислить приближенно площадь фигуры, ограниченной осью х, прямыми х=1 и х=3 и кривой 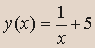, разбивая интервал изменения х на 10 частей и суммируя площади десяти прямоугольников с основанием 0,2 и высотой, равной значению функции в середине каждого интервала. Вычисление y(x) оформить в виде функции. Вычисление площади прямоугольника - в виде процедуры.
   
3. Выяснить, какая из букв, первая или последняя, встречается в заданном слове чаще.

Вариант № 6.

1. Составить программу, рисующую по главной диагонали (с правого верхнего угла в левый нижний угол) экрана 6 окружностей.
   
2. Два треугольника заданы координатами своих вершин А, В, С. Вычислить площади треугольников, не используя формулу Герона, и определить, какой треугольник имеет большую площадь. При решении задачи использовать следующие данные: для первого треугольника А(1,1), B(5,2), C(3,3); для второго треугольника А(2,5), B(4,3), C(6,4). Вычисление площади треугольника оформить в виде функции, а сравнение треугольников - в виде процедуры. Площадь треугольника вычисляется по формуле:
   S=1/2ЧЅ(X2-X1)Ч(Y3-Y1)-(X3-X1)Ч(Y2-Y1)Ѕ
   
3. Вычеркнуть из заданного слова все буквы, совпадающие с его последней буквой.
   

к оглавлению     на домашнюю